Contents

Ejemplo FDM con DFT - Tonos alejados

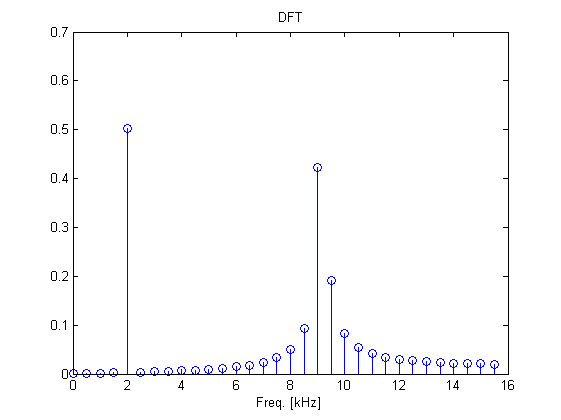
En este ejemplo vemos el espectro discreto (generado por una transformada discreta de Fourier o DFT) de dos tonos.

Si los tonos están alejados, las colas de su espectro no se afectan considerablemente

close all
Fs=32e3;    %Freq. muestreo
Nsamp=64;   %No puntos de DFT
t=0:1/Fs:(1/Fs)*(Nsamp-1);

fc1=2e3;    %Tono1
fc2=9.15e3; %Tono2

x=sin(2*pi*t*fc1)+sin(2*pi*t*fc2); % Genero la senyal en el tiempo
X=fft(x)/length(x); % La paso a frecuencia

f=(0:Nsamp/2-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
stem(f*1e-3,abs(X(1:Nsamp/2)))  % Muestro el espectro positivo.
title('DFT')
xlabel('Freq. [kHz]')

Ejemplo FDM con DFT - Tonos cercanos

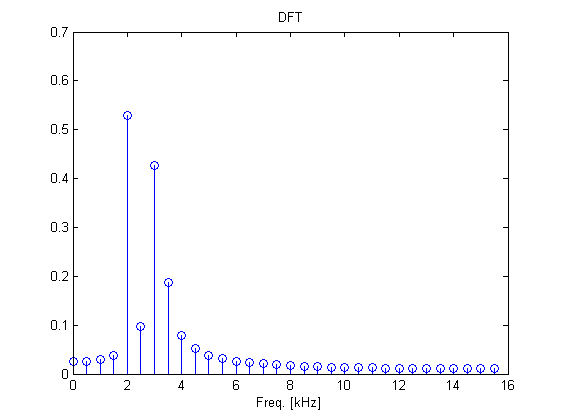
Si los tonos están muy cerca, se puede apreciar el efecto de su influencia en la amplitud del tono de 2kHz

close all
Fs=32e3;    %Freq. muestreo
Nsamp=64;   %No puntos de DFT
t=0:1/Fs:(1/Fs)*(Nsamp-1);

fc1=2e3;    %Tono1
fc2=3.15e3; %Tono2

x=sin(2*pi*t*fc1)+sin(2*pi*t*fc2); % Genero la senyal en el tiempo
X=fft(x)/length(x); % La paso a frecuencia

stem(f*1e-3,abs(X(1:Nsamp/2)))  % Muestro el espectro positivo.
title('DFT')
xlabel('Freq. [kHz]')

Ejemplo FDM con Transformada de Fourier Continua - Tonos alejados

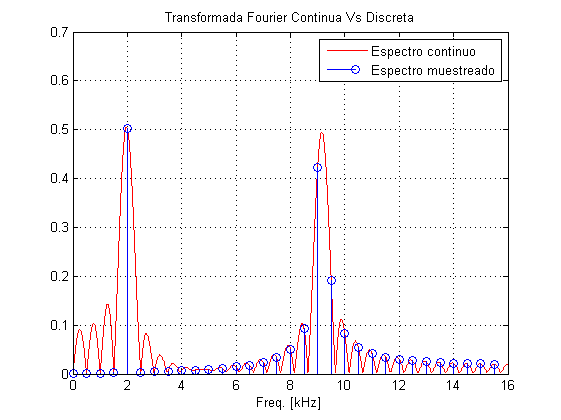
Si representamos la transformada de Fourier continua podemos ver el efecto que esta provocando su discretizacion.

Hay que recordar que la DFT es un muestreo discreto sobre la transformada de Fourier Continua

clear
Fs=32e3;    %Freq. muestreo
Nsamp=64;   %No puntos de DFT
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
t=0:1/Fs:(1/Fs)*(Nsamp-1);

fc1=2e3;    %Tono1
fc2=9.15e3; %Tono2

x=sin(2*pi*t*fc1)+sin(2*pi*t*fc2); % Genero la senyal en el tiempo


Xcont=fft(x,Nsampcont)/length(x); %Genero la TF continua
X=fft(x)/length(x);               %Genero la TF discreta

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2)),'r') %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X(1:Nsamp/2)))    %Dibujo espectro positivo de TF discreta

title('Transformada Fourier Continua Vs Discreta')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')
grid on

Ejemplo FDM con Transformada de Fourier Continua - Tonos cercanos

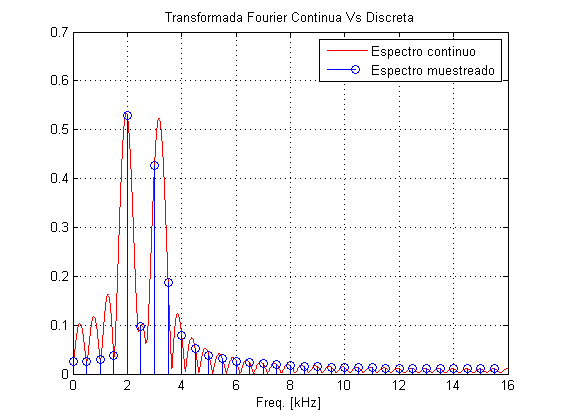
Al acercarse los tonos se puede ver la influencia de las colas

clear
Fs=32e3;    %Freq. muestreo
Nsamp=64;   %No puntos de DFT
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
t=0:1/Fs:(1/Fs)*(Nsamp-1);

fc1=2e3;    %Tono1
fc2=3.15e3; %Tono2

x=sin(2*pi*t*fc1)+sin(2*pi*t*fc2); % Genero la senyal en el tiempo


Xcont=fft(x,Nsampcont)/length(x); %Genero la TF continua
X=fft(x)/length(x);               %Genero la TF discreta

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2)),'r') %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X(1:Nsamp/2)))    %Dibujo espectro positivo de TF discreta

title('Transformada Fourier Continua Vs Discreta')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')
grid on

Ejemplo OFDM

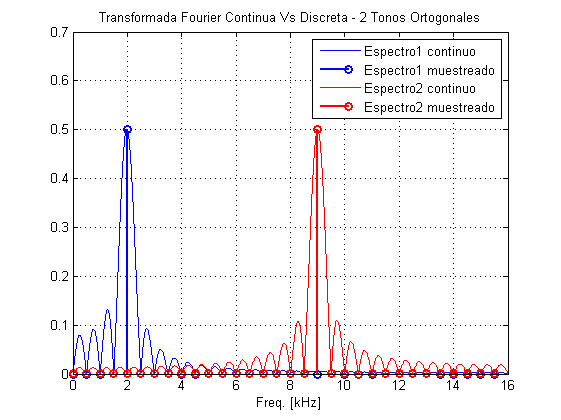
La ortogonalidad se consiegue utilizando tonos cuyos ceros del espectro se solapen en frecuencia. Esto provocara nula interferencia entre ellos.

En este ejemplo vemos dos tonos independientes. Observe como, si las frecuencias de los mismos se eligen con cuidado, no hay interferencias entre ellos (la posicion de cada tono coincide con un nulo del otro tono)

clear
Fs=32e3;    %Freq. muestreo
Nsamp=64;   %No puntos de DFT
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
t=0:1/Fs:(1/Fs)*(Nsamp-1);

fc1=2e3;    %Tono1
fc2=9e3; %Tono2

x1 = sin(2*pi*t*fc1);
x2 = sin(2*pi*t*fc2); %


X1cont=fft(x1,Nsampcont)/length(x1); %Genero la TF continua
X1=fft(x1)/length(x1);               %Genero la TF discreta

X2cont=fft(x2,Nsampcont)/length(x2); %Genero la TF continua
X2=fft(x2)/length(x2);               %Genero la TF discreta

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(X1cont(1:Nsampcont/2))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X1(1:Nsamp/2)),'LineWidth',2)    %Dibujo espectro positivo de TF discreta

plot(1e-3*fcont(1:length(fcont)/2),abs(X2cont(1:Nsampcont/2)),'r') %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X2(1:Nsamp/2)),'r','LineWidth',2)    %Dibujo espectro positivo de TF discreta


title('Transformada Fourier Continua Vs Discreta - 2 Tonos Ortogonales')
legend('Espectro1 continuo','Espectro1 muestreado','Espectro2 continuo','Espectro2 muestreado')
xlabel('Freq. [kHz]')
grid on

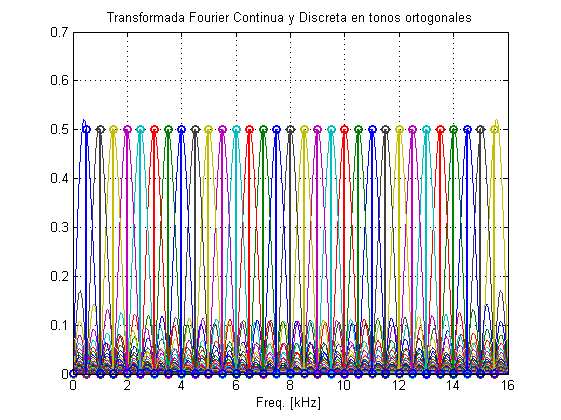
Ejemplo OFDM para todos los tonos posibles

%Todos los tonos cuya frecuencia sea m*Fs/Nsamp con m=0,1,...Nsamp-1
%tendrán un número de periodos entero y por lo tanto no se interferirán entre ellos.
%
% Se puede, por tanto, utilizar Nsamp tonos diferentes de manera que no
% haya interferencias
%
%Esos tonos son:

tonos=(0:Nsamp-1)*Fs/Nsamp

% Representando la señal temporal se puede ver cómo efectivamente
% entran un número de ciclos entero:

Fcont=1e6;  %Frecuencia muy alta para simular las señales contínuas
tcont=0:1/Fcont:(1/Fs)*(Nsamp-1);
t=0:1/Fs:(1/Fs)*(Nsamp-1);
tonos = (0:Nsamp-1)*Fs/Nsamp;


x=sin(2*pi*t'*tonos);
X = fft(x)/length(x);

xcont=sin(2*pi*tcont'*tonos);
Xcont = fft(x,Nsampcont)/length(x);


fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2,:))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X(1:Nsamp/2,:)),'LineWidth',2)    %Dibujo espectro positivo de TF discreta

title('Transformada Fourier Continua y Discreta en tonos ortogonales')
xlabel('Freq. [kHz]')
grid on

tonos =

  Columns 1 through 6

           0         500        1000        1500        2000        2500

  Columns 7 through 12

        3000        3500        4000        4500        5000        5500

  Columns 13 through 18

        6000        6500        7000        7500        8000        8500

  Columns 19 through 24

        9000        9500       10000       10500       11000       11500

  Columns 25 through 30

       12000       12500       13000       13500       14000       14500

  Columns 31 through 36

       15000       15500       16000       16500       17000       17500

  Columns 37 through 42

       18000       18500       19000       19500       20000       20500

  Columns 43 through 48

       21000       21500       22000       22500       23000       23500

  Columns 49 through 54

       24000       24500       25000       25500       26000       26500

  Columns 55 through 60

       27000       27500       28000       28500       29000       29500

  Columns 61 through 64

       30000       30500       31000       31500

Published with MATLAB® 7.14