leakage_test

No leakage
Leakage
Muestreo en Frecuencia SIN Leakage
Muestreo en Frecuencia CON Leakage
Doble de puntos de muestreo
Doble de puntos de muestreo y doble Fs
Doble de puntos de muestreo y doble Fs con dos tonos

No leakage

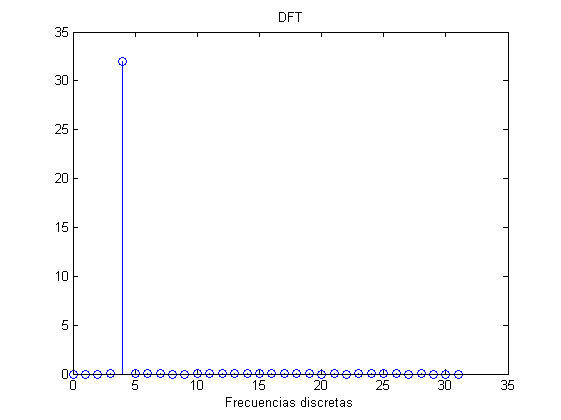
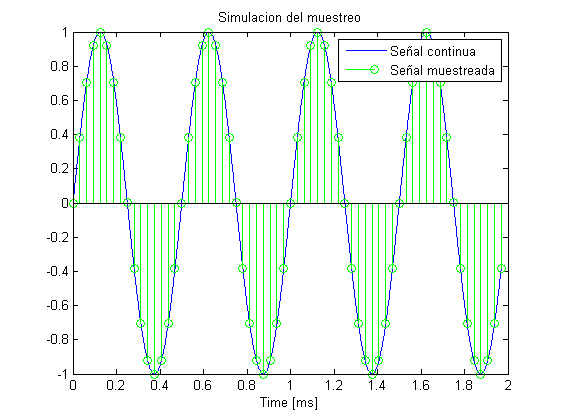
close all
Fs=32e3;    %Freq. muestreo
Nsamp=64;   %No puntos de DFT
t=0:1/Fs:(1/Fs)*(Nsamp-1);
f_tone=2e3;     %tone frequency
x=sin(2*pi*t*f_tone);
X=fft(x);
stem(0:(Nsamp/2)-1,abs(X(1:Nsamp/2)))
title('DFT')
xlabel('Frecuencias discretas')

%Todos los tonos cuya frecuencia sea m*Fs/Nsamp con m=0,1,...Nsamp-1
%tendrán un número de periodos entero y por lo tanto no tendrán leakage.
%Esos tonos son:

tonos=(0:Nsamp-1)*Fs/Nsamp

% Representando la señal temporal se puede ver cómo efectivamente
% entran un número de ciclos entero:

Fcont=1e6;  %Frecuencia muy alta para simular las señales contínuas
tcont=0:1/Fcont:(1/Fs)*(Nsamp-1);
xcont=sin(2*pi*tcont*f_tone);
figure,plot(tcont*1e3,xcont)
hold on
stem(t*1e3,x,'g')
legend('Señal continua','Señal muestreada')
title('Simulacion del muestreo')
xlabel('Time [ms]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

tonos =

  Columns 1 through 7

           0         500        1000        1500        2000        2500        3000

  Columns 8 through 14

        3500        4000        4500        5000        5500        6000        6500

  Columns 15 through 21

        7000        7500        8000        8500        9000        9500       10000

  Columns 22 through 28

       10500       11000       11500       12000       12500       13000       13500

  Columns 29 through 35

       14000       14500       15000       15500       16000       16500       17000

  Columns 36 through 42

       17500       18000       18500       19000       19500       20000       20500

  Columns 43 through 49

       21000       21500       22000       22500       23000       23500       24000

  Columns 50 through 56

       24500       25000       25500       26000       26500       27000       27500

  Columns 57 through 63

       28000       28500       29000       29500       30000       30500       31000

  Column 64

       31500


PowerFreq =

    0.5000


PowerTime =

    0.5079

Leakage

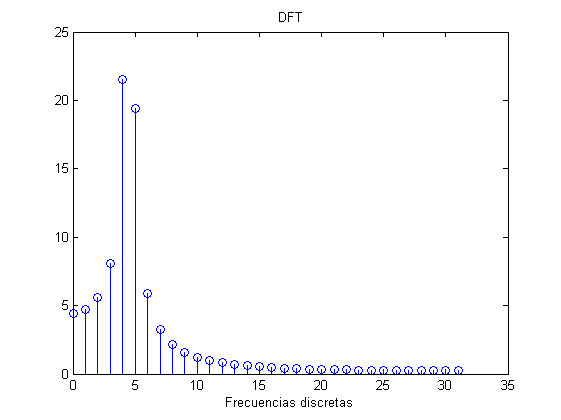
f_tone=2.25e3;     %tone frequency
x=sin(2*pi*t*f_tone);
X=fft(x);
figure,stem(0:(Nsamp/2)-1,abs(X(1:Nsamp/2)))
title('DFT')
xlabel('Frecuencias discretas')

%Al intentar representar un tono que no sea multiplo entero de Fs/Nsamp,
%vemos como se produce el "goteo"

% Representando la señal temporal se puede ver cómo efectivamente
% entran un número de ciclos entero:

Fcont=1e6;  %Frecuencia muy alta para simular las señales contínuas
tcont=0:1/Fcont:(1/Fs)*(Nsamp-1);
xcont=sin(2*pi*tcont*f_tone);
figure,plot(tcont*1e3,xcont)
hold on
stem(t*1e3,x,'g')
legend('Señal continua','Señal muestreada')
title('Simulacion del muestreo')
xlabel('Time [ms]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

PowerFreq =

    0.5000


PowerTime =

    0.5030

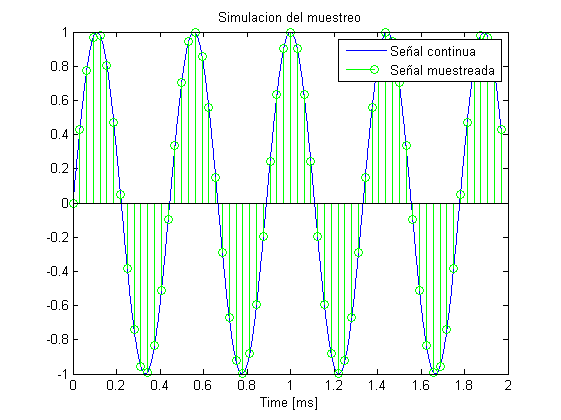
Muestreo en Frecuencia SIN Leakage

Veamos ahora cómo se produce el muestreo en frequencia

f_tone=2.5e3;     %tone frequency a una frecuencia válida

x=sin(2*pi*t*f_tone); %Genero la señal temporal
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
Xcont=fft(x,Nsampcont); %Genero la TF continua
X=fft(x);               %Genero la TF discreta

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X(1:Nsamp/2)),'g')    %Dibujo espectro positivo de TF discreta

title('Muestro en frecuencia con Leakage')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

PowerFreq =

    0.5000


PowerTime =

    0.5079

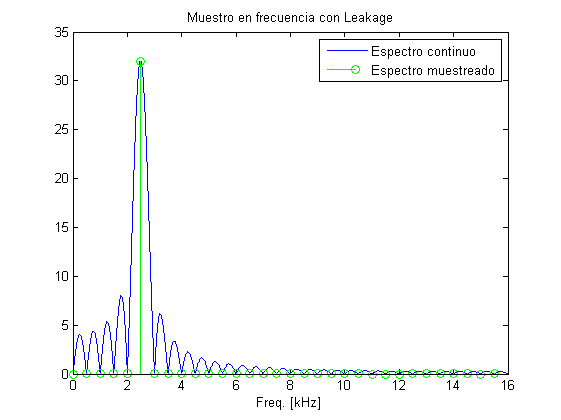
Muestreo en Frecuencia CON Leakage

Veamos ahora cómo se produce el muestreo en frequencia

f_tone=2.25e3;     %tone frequency a una frecuencia NO válida

x=sin(2*pi*t*f_tone); %Genero la señal temporal
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
Xcont=fft(x,Nsampcont); %Genero la TF continua
X=fft(x);               %Genero la TF discreta

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp-1)*Fs/Nsamp;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp/2),abs(X(1:Nsamp/2)),'g')    %Dibujo espectro positivo de TF discreta

title('Muestro en frecuencia sin Leakage')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

PowerFreq =

    0.5000


PowerTime =

    0.5030

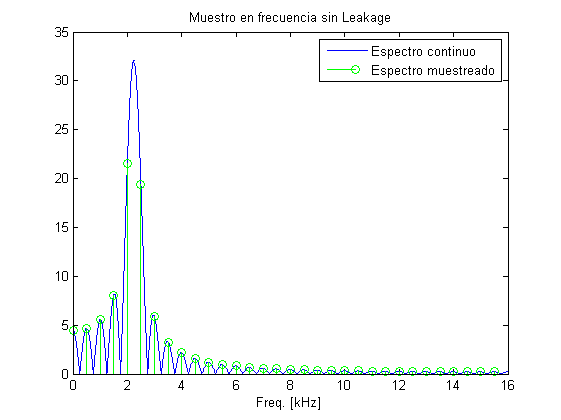
Doble de puntos de muestreo

Si únicamente doblo el número de muestras, estas me caerán no solo en los nulos de los lóbulos secundarios sino también en los máximos, pues estoy metiendo el doble de puntos en el mismo espectro

f_tone=2.5e3;     %tone frequency a una frecuencia válida
Nsamp2=2*Nsamp;

t=0:1/Fs:(1/Fs)*(Nsamp2-1);

x=sin(2*pi*t*f_tone); %Genero la señal temporal
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
Xcont=fft(x,Nsampcont); %Genero la TF continua
X=fft(x,Nsamp2);               %Genero la TF discreta con el doble de puntos

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp2-1)*Fs/Nsamp2;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp2/2),abs(X(1:Nsamp2/2)),'g')    %Dibujo espectro positivo de TF discreta

title('Muestro en frecuencia con 2*Nsamp --> Leakage')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

PowerFreq =

    0.5000


PowerTime =

    0.5039

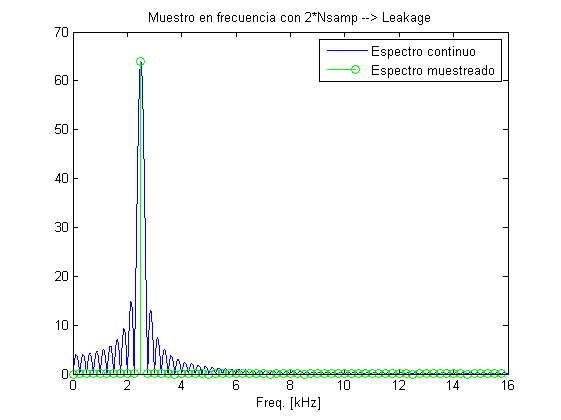
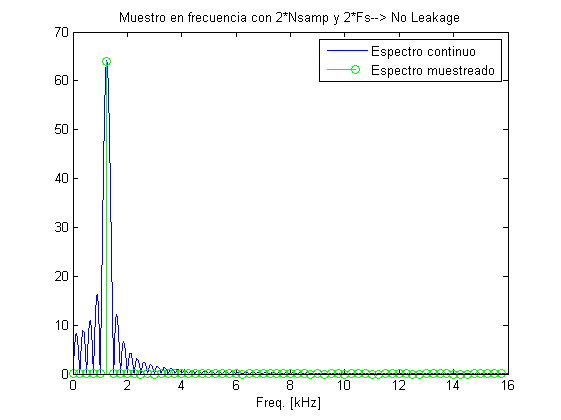
Doble de puntos de muestreo y doble Fs

Al doblar tamibén la frecuencia de muestreo obligo a "estirar" el doble los lóbulso secundarios, de manera que ahora todas las muestras caen en nulos (excepto la del tono)

f_tone=2.5e3;     %tone frequency a una frecuencia válida
Nsamp2=2*Nsamp;
Fs2=2*Fs;

t=0:1/Fs2:(1/Fs2)*(Nsamp2-1);

x=sin(2*pi*t*f_tone); %Genero la señal temporal
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
Xcont=fft(x,Nsampcont); %Genero la TF continua
X=fft(x,Nsamp2);               %Genero la TF discreta con el doble de puntos

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp2-1)*Fs/Nsamp2;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp2/2),abs(X(1:Nsamp2/2)),'g')    %Dibujo espectro positivo de TF discreta

title('Muestro en frecuencia con 2*Nsamp y 2*Fs--> No Leakage')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

PowerFreq =

    0.5000


PowerTime =

    0.5039

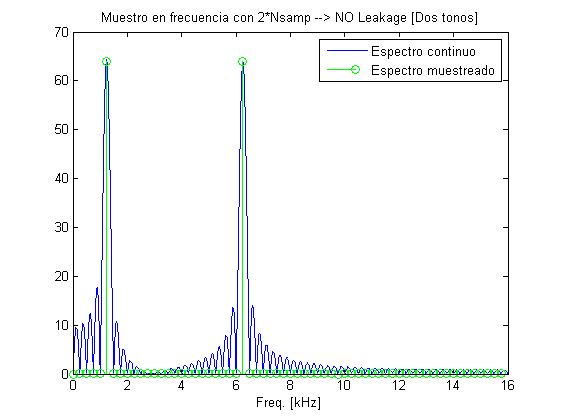
Doble de puntos de muestreo y doble Fs con dos tonos

Metamos ahora dos tonos para ver que todo sigue funcionando

f_tone1=2.5e3;     %tone frequency a una frecuencia válida
f_tone2=12.5e3;     %tone frequency a una frecuencia válida
Nsamp2=2*Nsamp;
Fs2=2*Fs;

t=0:1/Fs2:(1/Fs2)*(Nsamp2-1);

x=sin(2*pi*t*f_tone1)+sin(2*pi*t*f_tone2); %Genero la señal temporal
Nsampcont=2^20;         %numero de muestras alto para simular una TF continua
Xcont=fft(x,Nsampcont); %Genero la TF continua
X=fft(x,Nsamp2);               %Genero la TF discreta con el doble de puntos

fcont=(0:Nsampcont-1)*Fs/Nsampcont; %Frecuencias para represetar la TF continua
figure,
plot(1e-3*fcont(1:length(fcont)/2),abs(Xcont(1:Nsampcont/2))) %Dibujo espectro positivo de TF continua
f=(0:Nsamp2-1)*Fs/Nsamp2;         %Calculo frecuencas para la TF discreta
hold on
stem(1e-3*f(1:Nsamp2/2),abs(X(1:Nsamp2/2)),'g')    %Dibujo espectro positivo de TF discreta

title('Muestro en frecuencia con 2*Nsamp --> NO Leakage [Dos tonos]')
legend('Espectro continuo','Espectro muestreado')
xlabel('Freq. [kHz]')

PowerFreq=sum(abs(X).^2)/length(X)^2
PowerTime=var(x)

PowerFreq =

    1.0000


PowerTime =

    1.0079

Contents